 Bloomberg Excel Pricing Risk Sheet – FX Currency Forward Option Vanilla Analog
Bloomberg Excel Pricing Risk Sheet – FX Currency Forward Option Vanilla Analog$100.00$50.00Bloomberg Excel Pricing Risk Sheet – FX Currency Forward Option Vanilla Analog Replicate Bloomberg OVML Function in Excel Requires Bloomberg API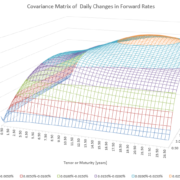 Derivative Pricing for Interest Rate Derivatives under Heath-Jarrow-Morton (HJM) Framework for Term Structure of Interest Rates with Principal Components Analysis (PCA), Monte Carlo Simulation (MCS), Credit Valuation Adjustment (CVA)
Derivative Pricing for Interest Rate Derivatives under Heath-Jarrow-Morton (HJM) Framework for Term Structure of Interest Rates with Principal Components Analysis (PCA), Monte Carlo Simulation (MCS), Credit Valuation Adjustment (CVA)$2,500.00$2,000.00Derivative Pricing for Interest Rate Derivatives under Heath-Jarrow-Morton (HJM) Framework for Term Structure of Interest Rates with Principal Components Analysis (PCA), Monte Carlo Simulation (MCS), Credit Valuation Adjustment (CVA) Package comes with:- Excel Workbook (.xlsm) Implementation
- With Sample Historical Forward Rates Term Structure from Bank of England
- With Differentiated Forward Rates
- With Covariance Matrix and Plot of Differentiated Forward Rates
- With Principal Component Analysis (PCA) of the Covariance Matrix
- VBA Function to Extract Eigen-Vectors
- VBA Function to Extract Eigen-Values
- 1-Click to Sort Results by Eigen-Values
- Volatility Response of Top 3 Factors (Level, Slope, Curvature)
- Volatility Term Structure for Top 3 Factors
- Volatility Fitting
- Factor 1 = Level = Constant
- Factor 2 = Slope = Polynomial, 1-Click Regression
- Factor 3 = Curvature = Polynomial, 1-Click Regression
- Monte Carlo Simulation (MCS) with Credit Valuation Adjustment (CVA)
- Simulate 1 time
- Simulate n times
- Calculate Average of n Simulations
- Get Simulated Prices for
- Zero-Coupon Bond
- Caplet
- Floorlet
- Forward Rate Agreement (FRA)
- Cap
- Floor
- Payer Swap
- Receiver Swap
- Select the derivative (from above list) for CVA adjustment
- Price before adjustment
- CVA adjustment
- Price after CVA-adjustment
- All VBA modules
- are NOT password protected
- are fully exposed for your modification
- well commented
- Basic User Guide
- Basic instructions on how to use the Excel Workbook Implementation
- In Word (.docx) format
- In PDF (.pdf) format
- Mathematical Theory and Code Guide
- Full explanation of the model with mathematical formulas and derivations
- Full explanation of code
- In Word (.docx) format
- In PDF (.pdf) format
- Excel Workbook (.xlsm) Implementation
 Equity Index Participation
Equity Index Participation$300.00$200.00Equity Index Participation Given a specified equity ticker, list the indices which contain it, and the corresponding weight of the ticker within each index. Excel Automated Trading Execution Spreadsheet for Interactive Brokers (IB) Trader Workstation (TWS)
Excel Automated Trading Execution Spreadsheet for Interactive Brokers (IB) Trader Workstation (TWS)$3,000.00$555.00This solution provides a start for automated trading execution on Interactive Brokers (IB) Trader Workstation (TWS). Market Orders, Market-on-Touch Order, Limits Orders, Trailing Limit Orders The download comes complete with:- Installation package:
- TWS API Installer [TWS API Install 971.06.msi]
- TWS Installer [tws-latest-windows-x86.exe]
- Step-by-step Installation Instructions [_installation_instructions.pdf]
- Excel Spreadsheet [TwsDde_971.06_20160906_2222_QB001.xls]
- Installation package:
 Excel Historical Data Downloader for Interactive Brokers (IB) Trader Workstation (TWS)$188.00This solution provides a historical time-series downloader in Excel for Interactive Brokers (IB) Trader Workstation (TWS). It provides the user with one-click solution to download historical data from IB.
Excel Historical Data Downloader for Interactive Brokers (IB) Trader Workstation (TWS)$188.00This solution provides a historical time-series downloader in Excel for Interactive Brokers (IB) Trader Workstation (TWS). It provides the user with one-click solution to download historical data from IB.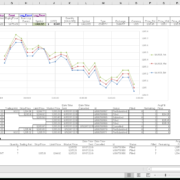 Excel Trading Execution Template for Interactive Brokers (IB) Trader Workstation (TWS)
Excel Trading Execution Template for Interactive Brokers (IB) Trader Workstation (TWS)$1,000.00$888.00URL to demonstration video: https://youtu.be/bYxhVcQ_x7I This solution provides a trading execution template in Excel for Interactive Brokers (IB) Trader Workstation (TWS). It provides the user with one-click execution of the following BUY and SELL order types:- (Buy/Sell) Market Orders
- (Buy/Sell) Limit Orders
- With user-specified Limit Price
- (Buy/Sell) Stop Limit Orders
- With user-specified Limit Price, Stop Price
- (Buy/Sell) Trailing Stop Limit Orders
- With user-specified Limit Price, Stop Price, Trailing Amount
 Loan Mortgage Monthly Payment Calculator
Loan Mortgage Monthly Payment Calculator$5.00$1.00This Excel spreadsheet calculates the monthly payment for a standard loan or mortgage. It uses the =PMT() function in excel. Requirements:- Microsoft Excel 2013
- and earlier versions that support =PMT() function.
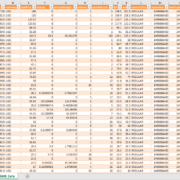
 Option Chain Downloader$555.00This Excel spreadsheet loads option chain data for any ticker available on finance.yahoo.com and/or finance.google.com. URL to demonstration video: https://youtu.be/tDAnbuk5A90 Here are some features:
Option Chain Downloader$555.00This Excel spreadsheet loads option chain data for any ticker available on finance.yahoo.com and/or finance.google.com. URL to demonstration video: https://youtu.be/tDAnbuk5A90 Here are some features:- Loads the full option chain for a list of tickers
- Each ticker will have it's own output sheet
- Each sheet includes all expiration dates for the ticker
- Each expiration date will Includes put and calls in a straddle view
- All strikes are included, and sorted in ascending order
- Each expiration date will Includes put and calls in a straddle view
- Each sheet includes all expiration dates for the ticker
- Note that each ticker takes a typical 3-5 minutes to load, depending on
- Number of expiration dates
- Number of strikes
- Internet connection speed
- Each ticker will have it's own output sheet
- Separate functionality is also available if you wish to load on a per ticker basis
- Live Price for any* ticker
- Historical Prices for any* ticker
- Option Chain for any* ticker on finance.yahoo.com (User will input one ticker at a time)
- Option Chain for any expiration dates (It will search for all available expiration dates, and you can select one from the list)
- Option Chain for ALL expiration dates with 1-click.
- Option Chain for puts only, or calls only, or puts and calls in a straddle view (with strikes sorted in ascending order)
- Option Chain for any strike (Given the ticker, expiration date, and put or call or both, it will load the option chain for all strikes)
- Loads the full option chain for a list of tickers
 Option Chain Downloader v01$288.00This Excel spreadsheet loads option chain data for any ticker available on finance.yahoo.com. URL to demonstration video: https://youtu.be/gYSEwAvOdWM Here are some features:
Option Chain Downloader v01$288.00This Excel spreadsheet loads option chain data for any ticker available on finance.yahoo.com. URL to demonstration video: https://youtu.be/gYSEwAvOdWM Here are some features:- Option Chain for any* ticker on finance.yahoo.com (User will input one ticker at a time)
- Option Chain for any expiration dates (It will search for all available expiration dates, and you can select one from the list)
- Option Chain for puts and calls (User can select either one)
- Option Chain for any strike (Given the ticker, expiration date, and put or call, it will load the option chain for all strikes)
